Sykkelrammekonstruksjon Analyse av krefter

		For å kunne dimensjonere rørtykkelser, sveis og andre deler av rammen er man nødt til å se på de kreftene som virker. Det vil fort slå sprekker i sveisesømmer og rammerør hvis de ikke er dimensjonert for det de skal tåle. Vi har i dette prosjektet tatt utgangspunkt i en 57cm landeveisramme. Vi har satt disse begrensningene for hva rammen maksimalt skal tåle. Begrensningene er en rytter opp til 105kg. Sykkelen skal maksimalt tåle at man hopper ned fra en høyde på 25cm. Vi legger selvfølgelig inn en sikkerhetsfaktor, så selv om du veier 107kg og hopper fra 30cm, så skal ikke rammen gå i brudd for det :) Vi vil gi deg et lite innblikk her i hvordan man går frem for å analysere kreftene.
		Rammegeometri
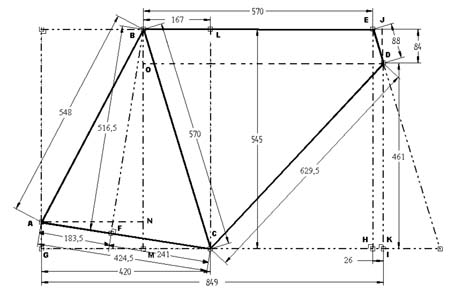
		Først må vi finne lengden av alle rør. Tar utgangspunkt i at styrerøret og seterøret har en helling på 73 grader, avstanden fra senter av krank til krysningspunktet mellom senterlinjen fra overrøret og senterlinjen fra seterøret er 570mm og lengden av overrøret er 570mm. Rammen er bestemt av disse målene, da er det bare å regne ut resten og presentere det slik:
		De uthvede svarte linjene er senterlinjene i rørene. På samme måte finner man vinklene man mangler.
		Tre belastningssituasjoner
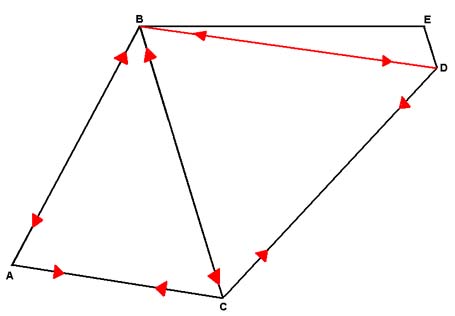
		Vi har studert 3 forskjellige belastningssituasjoner. Hver av belastningssituasjonene gjør at enkelte rør blir utsatt for stor belastning. Ved å simulere disse situasjonene i et matematisk program, vil vi se hvilken belastningssituasjon som gir størst kraft i hvert rør. Det er de størst opptredende kreftene vi er ute etter, det er disse vi må bruke for dimensjonering. De tre belastningssituasjonene er: 1: Rytteren har all sin tyngde på setet. 2: Rytteren sitter på sete og holder hendene på styret. 3: Rytteren står og tråkker (antar kun belastning i krank,neglisjerer kraft på styret). Vi skal beregnet dette med en metode som heter fagverksmetoden. for å sette opp ligningene trenger vi å anta hva slags krefter som oppstår i rørene, trykk eller strekk.
		Her er kreftene med sine antatte invirkninger på rørene tegnet inn. Piler som peker fra hverandre indikerer trykk og piler som peker fra hverandre indikerer strekk. Den røde linjen man ser på illustrasjonen over er kun en fiktiv stav. Uten å gå så nøye inn på det her, så lar ikke rammen seg beregne uten å ha denne til hjelp. Kraften man får i denne staven som ikke er der vil bli dekomponert over i stavene som ikke har krefter tegnet inn. Når man har satt opp dette slik, kan man sette opp ligninger for hvert krysningspunkt mellom rørene. Som vi ser på illustrasjonen er det 5 slike krysningspunkter. For at ikke rammen eller konstruksjoner generelt skal gå i budd, må kreftene være lik null. Er ikke kreftene lik null, vil det gå galt. Kan gi et lite eksempel på det. Hvis du står og dytter på en vegg med en viss kraft, så vil veggen virke tilbake på deg med en like stor og motsatt rettet kraft. Da er summen av kreftene lik null. I det du dytter så hardt at veggen faller ned, så er/var ikke kreftene lengre lik null. Du har da påført veggen en kraft som er større enn det den kan tåle. Det er det prinsippet som blir brukt ved dimensjonering. For å bestemme kreftene i alle rørene så beregner vi fra krysningspunkt til krysningspunkt til vi er rundt til der vi startet. Skal vise her hvordan et krysningspunkt vil se ut.
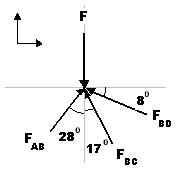
		Over ser man krysningspunktet med hvordan kreftene fra rørene vil angripe i krysningspunkt B. F, er kraften fra sykkelrytteren. De andre kreftene er rørkreftene i rørene. Som man ser av ligningene så er summen av kreftene lik 0. Det som er vist over er den desidert største oppgaven her, det å bestemme kreftene i rørene. Det er ganske mye mer man må gjøre etter å funnet kreftene i alle rørene, men det skal jeg ikke gå nærmere inn på her.
		Det at syklisten sitter i ro på setet gir ikke de største kreftene i rørene. De største kreftene oppstår gjerne ved slag og støt. Så vi beregner den kraften syklisten vil utsette sykkelen for i et hopp fra en høyde på 25cm. Antar da at dekkene får en sammentrykning på 10mm når syklisten treffer bakken. Da kan man enkelt ved bruk av energiligninger finne den kraften syklisten utsetter sykkelen for. Nå som vi allerede har satt opp ligningene for situasjonen der syklisten kun belaster sykkelen på sete, så kan denne nye utregnede ekstrembelastningen settes inn for kraften F. Dataprogrammet hvor vi har satt ligningene inn gir oss raskt de nye kreftene som oppstår i rørene.
		Satte denne ekstremverdien inn i programmet som er satt opp i det matematiske programmet Maple. Da får vi ekstremkreftene i rørene, alt er i Newton. Det ene negative fortegnet man ser over, viser bare at kreftene i røret er motsatt av det som er antatt. Vi gjør samme prosedyre for alle de tre belastningssituasjonene og finner de største opptredende kreftene. Nå kan vi dimensjonere rørene.
		Det er mange standard dimensjoner på en sykkel, så man må ta høyde for disse, særlig når det gjelder seterøret. Litt kjedelig å dimensjonere feil her, slik at man ikke får tak i noen setepinne som passer, eller krankgir som passer rundt røret. Men underrøret har ingen standard dimensjoner knyttet til seg. Først bestemmer vi hvor stort tverrsnittsarealet må bli, fra denne formelen.
		Spenningen [N/mm^2] er definert som kraft delt på tverrsnittsareal, som er den første ligningen over. Vi må passe på å holde oss innenfor flytegrensen til materialet, ellers vi materialet bli deformert når man legger på belastning. Løser ligningen med hensyn på tverrsnittsarealet,A. Finner da arealet ved å dele kraften som oppstår i røret på flytegrensen, eller det vi gjør, den største spenningen vi vil tillate i røret. Nå kan vi bestemme f.eks ytre diameter, da må vi bare bestemme indre diameter slik at tverrsnittsarealet er oppfylt. Røret er nå dimensjonert, iallfall for å tåle den kraften det blir utsatt for. Når vi skal se på stivhet i ramme, må vi se på motstandsmomentet, men det er en annen historie :)
		Tilbake
		Skrevet av Sykkelsiden.no April 2004, Copyright